Plotting maps

As test data we use the CMIP6 Scenarios.

using Zarr, YAXArrays, Dates
using DimensionalData
using GLMakie, GeoMakie
using GLMakie.GeometryBasics

store ="gs://cmip6/CMIP6/ScenarioMIP/DKRZ/MPI-ESM1-2-HR/ssp585/r1i1p1f1/3hr/tas/gn/v20190710/"

"gs://cmip6/CMIP6/ScenarioMIP/DKRZ/MPI-ESM1-2-HR/ssp585/r1i1p1f1/3hr/tas/gn/v20190710/"

julia> g = open_dataset(zopen(store, consolidated=true))

YAXArray Dataset
Shared Axes:
None
Variables: 
height

Variables with additional axes:
  Additional Axes: 
  (↓ lon  Sampled{Float64} 0.0:0.9375:359.0625 ForwardOrdered Regular Points,
  → lat  Sampled{Float64} [-89.28422753251364, -88.35700351866494, …, 88.35700351866494, 89.28422753251364] ForwardOrdered Irregular Points,
  ↗ time Sampled{DateTime} [2015-01-01T03:00:00, …, 2101-01-01T00:00:00] ForwardOrdered Irregular Points)
  Variables: 
  tas

Properties: Dict{String, Any}("initialization_index" => 1, "realm" => "atmos", "variable_id" => "tas", "external_variables" => "areacella", "branch_time_in_child" => 60265.0, "data_specs_version" => "01.00.30", "history" => "2019-07-21T06:26:13Z ; CMOR rewrote data to be consistent with CMIP6, CF-1.7 CMIP-6.2 and CF standards.", "forcing_index" => 1, "parent_variant_label" => "r1i1p1f1", "table_id" => "3hr"…)

julia> c = g["tas"];

Subset, first time step

julia> ct1_slice = c[time = Near(Date("2015-01-01"))];

use lookup to get axis values

lon_d = lookup(ct1_slice, :lon)
lat_d = lookup(ct1_slice, :lat)
data_d = ct1_slice.data[:,:];

Heatmap plot

GLMakie.activate!()

fig, ax, plt = heatmap(ct1_slice; colormap = :seaborn_icefire_gradient,
    axis = (; aspect=DataAspect()),
    figure = (; size = (1200,600), fontsize=24))
fig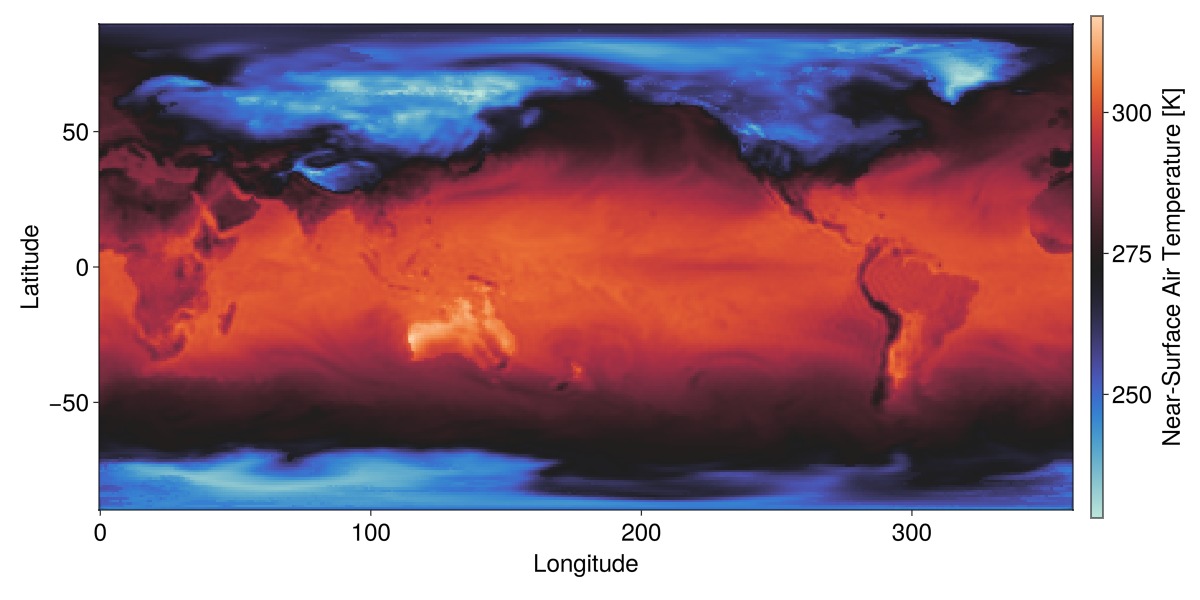

Wintri Projection

Some transformations

δlon = (lon_d[2] - lon_d[1])/2
nlon = lon_d .- 180 .+ δlon
ndata = circshift(data_d, (192,1))

and add Coastlines with GeoMakie.coastlines(),

fig = Figure(;size=(1200,600))
ax = GeoAxis(fig[1,1])
surface!(ax, nlon, lat_d, ndata; colormap = :seaborn_icefire_gradient, shading=false)
cl=lines!(ax, GeoMakie.coastlines(), color = :white, linewidth=0.85)
translate!(cl, 0, 0, 1000)
fig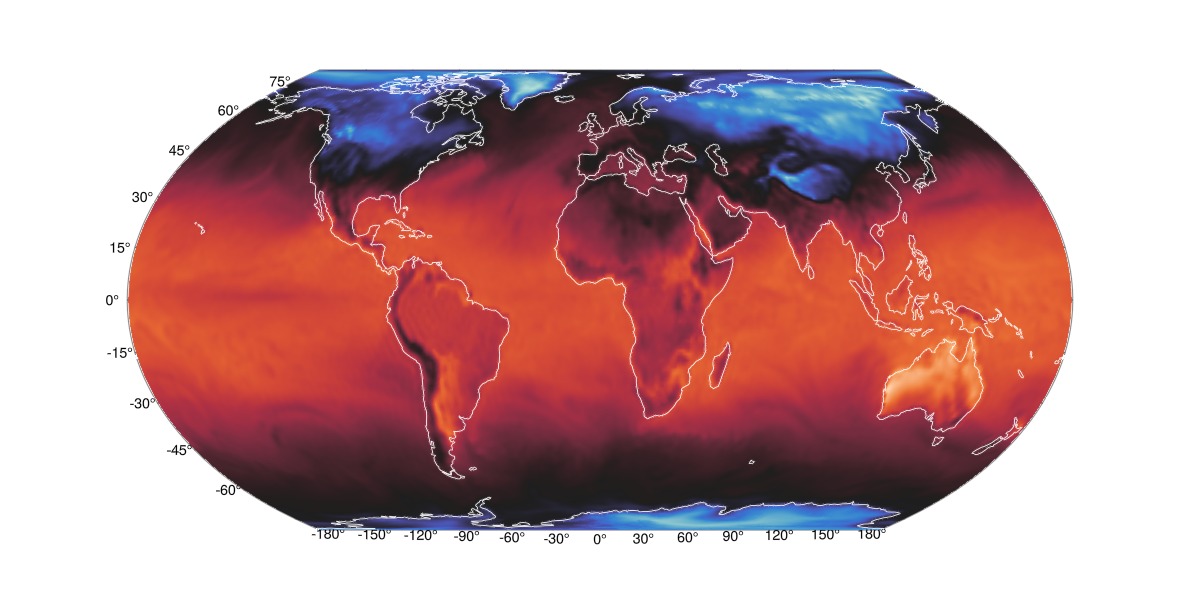

Moll projection

fig = Figure(; size=(1200,600))
ax = GeoAxis(fig[1,1]; dest = "+proj=moll")
surface!(ax, nlon, lat_d, ndata; colormap = :seaborn_icefire_gradient, shading=false)
cl=lines!(ax, GeoMakie.coastlines(), color = :white, linewidth=0.85)
translate!(cl, 0, 0, 1000)
fig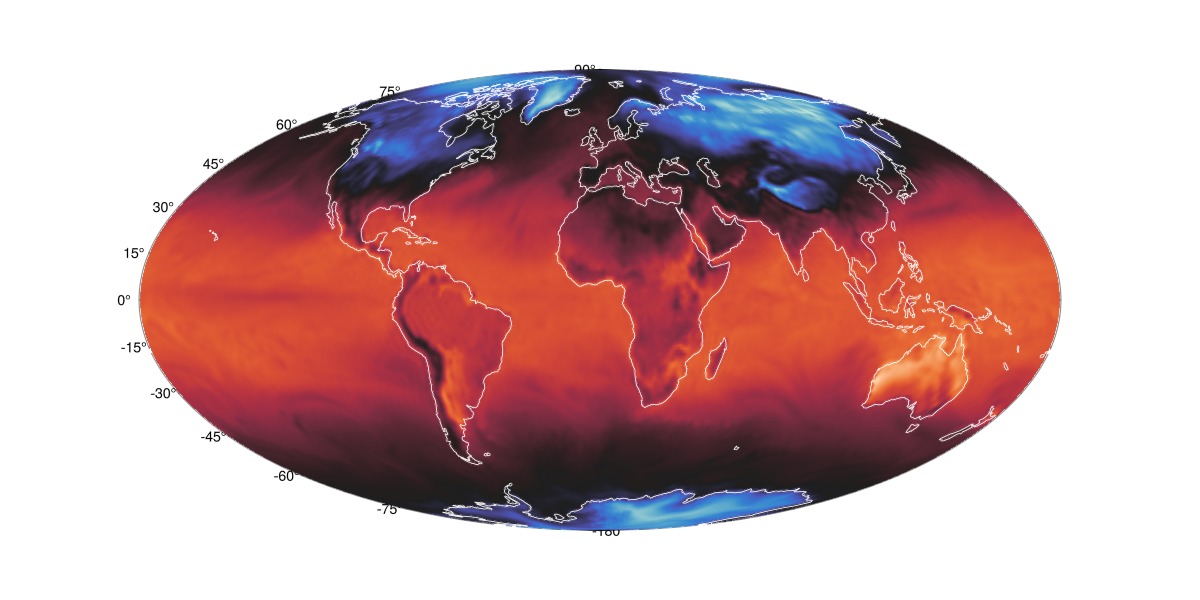

3D sphere plot

using GLMakie
using GLMakie.GeometryBasics
GLMakie.activate!()

ds = replace(ndata, missing =>NaN)
sphere = uv_normal_mesh(Tesselation(Sphere(Point3f(0), 1), 128))

fig = Figure(backgroundcolor=:grey25, size=(500,500))
ax = LScene(fig[1,1], show_axis=false)
mesh!(ax, sphere; color = ds'[end:-1:1,:], shading=false,
    colormap = :seaborn_icefire_gradient)
zoom!(ax.scene, cameracontrols(ax.scene), 0.5)
rotate!(ax.scene, 2.5)
fig

AlgebraOfGraphics.jl

INFO

From DimensionalData docs :

AlgebraOfGraphics.jl is a high-level plotting library built on top of Makie.jl that provides a declarative algebra for creating complex visualizations, similar to ggplot2's "grammar of graphics" in R. It allows you to construct plots using algebraic operations like * and +, making it easy to create sophisticated graphics with minimal code.

using YAXArrays, Zarr, Dates
using GLMakie
using AlgebraOfGraphics
using GLMakie.GeometryBasics
GLMakie.activate!()

let's continue using the cmip6 dataset

store ="gs://cmip6/CMIP6/ScenarioMIP/DKRZ/MPI-ESM1-2-HR/ssp585/r1i1p1f1/3hr/tas/gn/v20190710/"
g = open_dataset(zopen(store, consolidated=true))
c = g["tas"];

and let's focus on the first time step:

dim_data = readcubedata(c[time=1]); # read into memory first!

and now plot

data(dim_data) * mapping(:lon, :lat; color=:value) * visual(Scatter) |> draw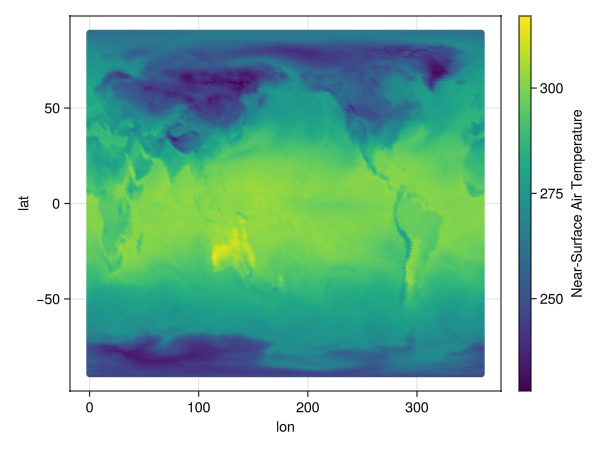

WARNING

Note that we are using a Scatter type per point and not the Heatmap one. There are workarounds for this, albeit cumbersome, so for now, let's keep this simpler syntax in mind along with the current approach being used.

set other attributes

plt = data(dim_data) * mapping(:lon, :lat; color=:value)
draw(plt * visual(Scatter, marker=:rect), scales(Color = (; colormap = :plasma));
    axis = (width = 600, height = 400, limits=(0, 360, -90, 90)))

Faceting

For this let's consider more time steps from our dataset:

using Dates
dim_time = c[time=DateTime("2015-01-01") .. DateTime("2015-01-01T21:00:00")] # subset 7 t steps

┌ 384×192×7 YAXArray{Float32, 3} ┐
├────────────────────────────────┴─────────────────────────────────────── dims ┐
  ↓ lon  Sampled{Float64} 0.0:0.9375:359.0625 ForwardOrdered Regular Points,
  → lat  Sampled{Float64} [-89.28422753251364, -88.35700351866494, …, 88.35700351866494, 89.28422753251364] ForwardOrdered Irregular Points,
  ↗ time Sampled{DateTime} [2015-01-01T03:00:00, …, 2015-01-01T21:00:00] ForwardOrdered Irregular Points
├──────────────────────────────────────────────────────────────────── metadata ┤
  Dict{String, Any} with 10 entries:
  "units"         => "K"
  "history"       => "2019-07-21T06:26:13Z altered by CMOR: Treated scalar dime…
  "name"          => "tas"
  "cell_methods"  => "area: mean time: point"
  "cell_measures" => "area: areacella"
  "long_name"     => "Near-Surface Air Temperature"
  "coordinates"   => "height"
  "standard_name" => "air_temperature"
  "_FillValue"    => 1.0f20
  "comment"       => "near-surface (usually, 2 meter) air temperature"
├─────────────────────────────────────────────────────────────── loaded lazily ┤
  data size: 1.97 MB
└──────────────────────────────────────────────────────────────────────────────┘

dim_time = readcubedata(dim_time); # read into memory first!

plt = data(dim_time) * mapping(:lon, :lat; color = :value, layout = :time => nonnumeric)
draw(plt * visual(Scatter, marker=:rect))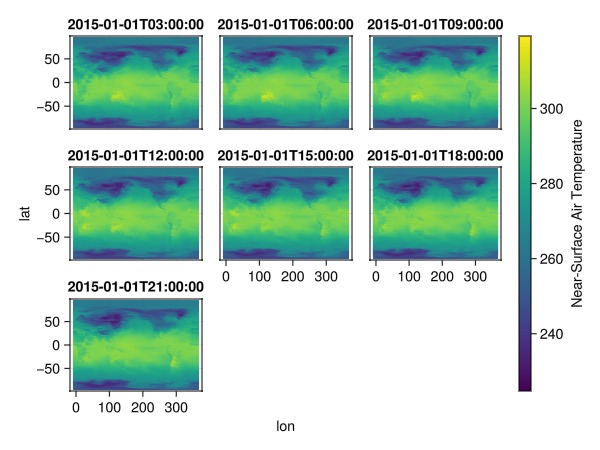

again, let's add some additional attributes

plt = data(dim_time) * mapping(:lon, :lat; color = :value, layout = :time => nonnumeric)
draw(plt * visual(Scatter, marker=:rect), scales(Color = (; colormap = :magma));
    axis = (; limits=(0, 360, -90, 90)),
    figure=(; size=(900,600)))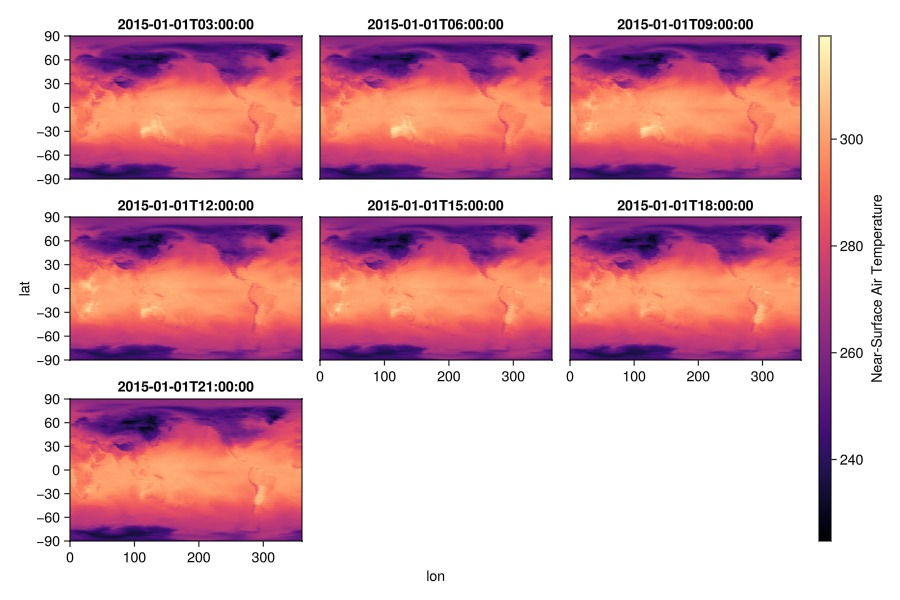

most Makie plot functions should work. See lines for example

plt = data(dim_data[lon=50..100]) * mapping(:lat, :value => "tas"; color=:value => "tas")
draw(plt * visual(Lines); figure=(; size=(650,400)))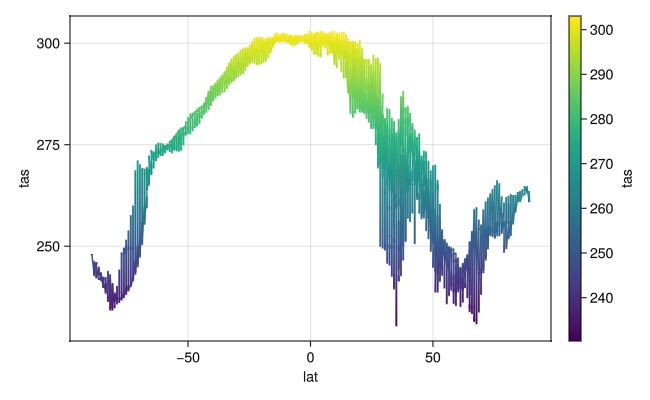

or faceting them

plt = data(dim_data[lon=50..59]) * mapping(:lat, :value => "tas"; color=:value => "tas",
    layout = :lon => nonnumeric)
draw(plt * visual(Lines); figure=(; size=(650,400)))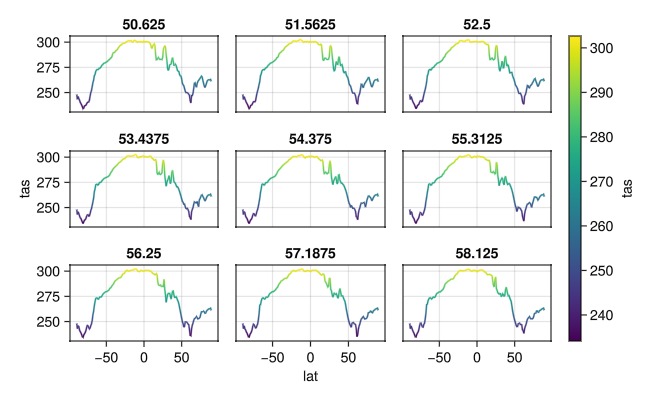

Time series

For this, let's load a little bit more of time steps

dim_series = c[time=DateTime("2015-01-01") .. DateTime("2015-01-04"), lon = 150 .. 157, lat = 0..1] |> readcubedata

┌ 8×1×24 YAXArray{Float32, 3} ┐
├─────────────────────────────┴────────────────────────────────────────── dims ┐
  ↓ lon  Sampled{Float64} 150.0:0.9375:156.5625 ForwardOrdered Regular Points,
  → lat  Sampled{Float64} [0.4675308904227747] ForwardOrdered Irregular Points,
  ↗ time Sampled{DateTime} [2015-01-01T03:00:00, …, 2015-01-04T00:00:00] ForwardOrdered Irregular Points
├──────────────────────────────────────────────────────────────────── metadata ┤
  Dict{String, Any} with 10 entries:
  "units"         => "K"
  "history"       => "2019-07-21T06:26:13Z altered by CMOR: Treated scalar dime…
  "name"          => "tas"
  "cell_methods"  => "area: mean time: point"
  "cell_measures" => "area: areacella"
  "long_name"     => "Near-Surface Air Temperature"
  "coordinates"   => "height"
  "standard_name" => "air_temperature"
  "_FillValue"    => 1.0f20
  "comment"       => "near-surface (usually, 2 meter) air temperature"
├──────────────────────────────────────────────────────────── loaded in memory ┤
  data size: 768.0 bytes
└──────────────────────────────────────────────────────────────────────────────┘

and plot

plt = data(dim_series) * mapping(:time, :value => "tas"; color=:lon => nonnumeric)
draw(plt * visual(ScatterLines), scales(Color = (; palette = :tableau_colorblind));
    figure=(; size=(800,400)))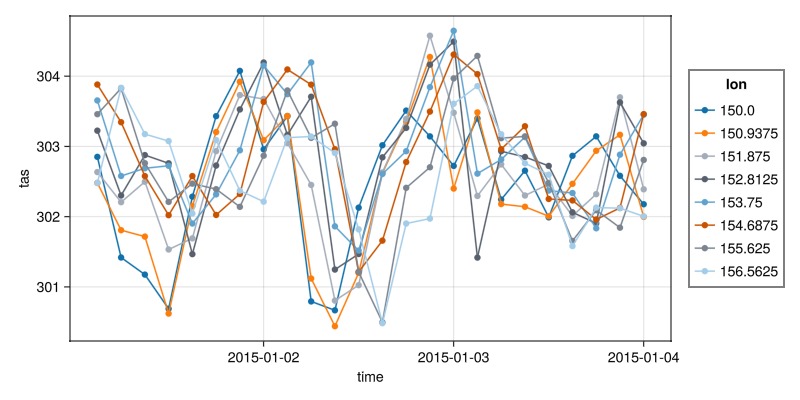

Analysis

Basic statistical analysis can also be done, for example:

specs = data(dim_data[lat=50..55]) * mapping(:lon, :value => "tas"; color=:lat => nonnumeric)
specs *= (smooth() + visual(Scatter))
draw(specs;  figure=(; size=(700,400)))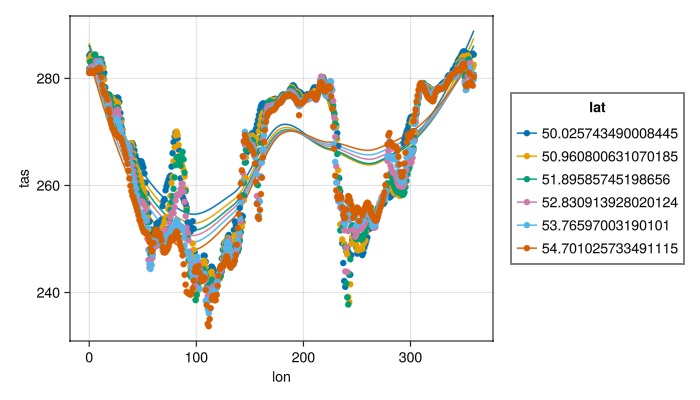

For more, visit AlgebraOfGraphics.jl.